Capítulo 4 Modelo Hidrológico

El diseño hidrológico para el control de aguas tiene como objetivo principal la mitigación de los efectos adversos causados por caudales altos. Se considera una creciente a cualquier caudal elevado que desborde los terraplenes, ya sean artificiales o naturales, debido a sus elevadas elevaciones y volúmenes (Chow, Maidment, and Mays 1994).

4.1 Cálculo de caudales

Ante la falta de información hidrológica en una zona en estudio, para hacer una estimación de los gastos de escurrimiento se recomiendan los métodos empíricos, ecuaciones que consideran uno o dos parámetros deducidos de una región o ciudad (CONAGUA 2019).

Los parámetros que se ocupan para los cálculos de las metodologías presentadas, son los siguientes.

El área de la cuenca es: 1.04 km²

El número de curva es: 93

La retención potencial máxima del suelo es: 19.12 mm

La abstracción inicial es: 3.82 mm .

El tiempo de concentración calculado por Kirpich para toda el área de estudio es: 0.41 horas o 24.66 minutos

El tiempo de retraso es: 0.25 horas

La duración efectiva es: 1.28 horas

El tiempo pico es: 0.89 horas

El tiempo base es: 2.37 horas

El coeficiente FRA es: 1

El FRA se calcula con la ecuación \[ FRA = 1.0 - 0.091293 \cdot \left(1.0 - e^{-0.005794 \cdot A}\right) \]

El tiempo de retraso se calcula con la ecuación \[ T~r~ = 0.6 \cdot \ T~c~ \]

La duración efectiva se calcula con la ecuación \[ de = 2 \cdot \sqrt{T~c~} \]

El tiempo pico se calcula con la ecuación \[ T~p~ = \frac{de}{2} + T~r~ \]

El tiempo base se calcula con la ecuación \[ T~b~ = 2.67 \cdot T~p~ \]

El número de curva se obtuvo de la tabla 2-2 ‘Número de curva para áreas urbanas’ del USDA TR 55.

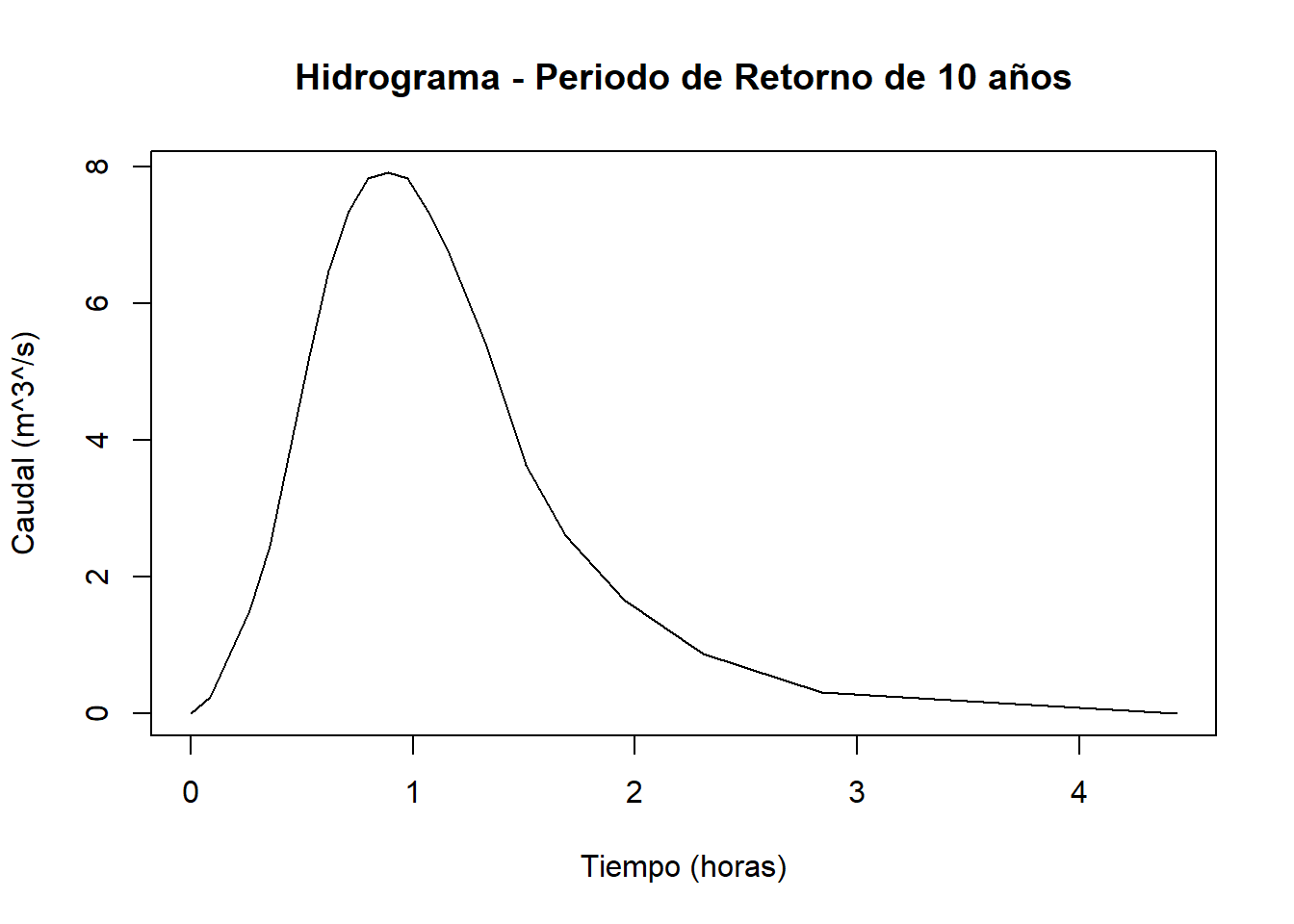
4.1.1 Caudal Q por HUT (Hidrograma Uniforme Triangular)

La técnica del hidrograma unitario tiene una base teórica y es bastante consistente, por ello ha alcanzado gran universalidad. El hidrograma unitario se define como el hidrograma de gasto resultante de una lluvia en exceso unitaria ocurriendo uniformemente sobre la cuenca y durante la duración unitaria especificada. La definición anterior limita a los 1,300 km², el tamaño máximo de las cuencas en las que el método puede ser aplicado sin ser subdivididas, ya que en tales cuencas es todavía muy probable que la lluvia procedente de un fenómeno no ciclónico iguale la magnitud de las crecientes originadas por las precipitaciones ciclónicas. \[ Q = \frac {0.208 * P_e * A} {T_p} \].

El USDA TR 55 explica como calcular S, la retención potencial máxima del suelo, con la ecuación \[ S = \frac{1000}{CN} - 10 \] en sistema inglés.

Tabla 4.1: Intensidades de lluvia (mm/hr)

	Tr_2	Tr_5	Tr_10	Tr_20	Tr_25	Tr_50	Tr_100	Tr_200	Tr_500	Tr_1000	Tr_2000	Tr_5000	Tr_10000
76.9342197345612	26.7917	29.8882	32.2306	34.573	35.3271	37.6695	40.012	42.3544	45.4509	47.7933	50.1357	53.2322	55.5746

Obtenemos la precipitación multiplicando la intensidad por la duración efectiva y luego corregimos el resultado con el parámetro FRA.

Tabla 4.2: Precipitaciones ajustadas (mm)

	Tr_2	Tr_5	Tr_10	Tr_20	Tr_25	Tr_50	Tr_100	Tr_200	Tr_500	Tr_1000	Tr_2000	Tr_5000	Tr_10000
76.9342197345612	34.3345	38.3028	41.3046	44.3065	45.2729	48.2748	51.2767	54.2786	58.2469	61.2488	64.2506	68.2189	71.2208

Tabla 4.3: Precipitaciones efectivas (mm)

	Tr_2	Tr_5	Tr_10	Tr_20	Tr_25	Tr_50	Tr_100	Tr_200	Tr_500	Tr_1000	Tr_2000	Tr_5000	Tr_10000
76.9342197345612	18.7573	22.1803	24.8205	27.4972	28.3657	31.0826	33.8252	36.5902	40.275	43.082	45.9037	49.6536	52.5037

El resultado final es la tabla de caudales calculados por HUT.

Tabla 4.4: Caudales (m³/s) calculados por HUT

	Tr_2	Tr_5	Tr_10	Tr_20	Tr_25	Tr_50	Tr_100	Tr_200	Tr_500	Tr_1000	Tr_2000	Tr_5000	Tr_10000
76.9342197345612	4.5667	5.4001	6.0429	6.6946	6.906	7.5675	8.2352	8.9084	9.8055	10.4889	11.1759	12.0889	12.7828

4.1.2 MÉTODO RACIONAL

La concepción fundamental del método Racional establece que la intensidad de lluvia i comienza instantáneamente y continúa indefinidamente, la cantidad de escurrImiento se va incrementando hasta alcanzar el tiempo de concentración (T_c), cuando toda la cuenca está contribuyendo al flujo en su salida. Por lo anterior, la intensidad i tiene una duración igual al T_c y corresponde al periodo de retomo de la creciente o gasto máximo que se estima. El cociente entre el producto de la intensidad de lluvia i por el área de cuenca A y el gasto máximo Q, que ocurre al llegar al T_c, se denomina coeficiente de escurrimiento C y lógicamente varía de cero a uno. Con base al Manual de CONAGUA se determina que el coeficiente de escurrimiento para un uso de terreno industrial denso para un período de retorno de 10 años es ‘0.85’.

\[ 0.278 * C * I * A \]

Después de realizar las operaciones, el método racional arroja los siguientes caudales.

Tabla 4.5: Caudales (m³/s) calculados por el método Racional

	Tr_2	Tr_5	Tr_10	Tr_20	Tr_25	Tr_50	Tr_100	Tr_200	Tr_500	Tr_1000	Tr_2000	Tr_5000	Tr_10000
76.9342197345612	6.5784	7.3387	7.9139	8.489	8.6742	9.2494	9.8245	10.3997	11.16	11.7351	12.3103	13.0706	13.6458

4.1.3 METODO VEN TE CHOW

Este método es aplicable a cuencas menores de 24.3 km², está basado en la teoría del hidrograma unitario y de la curva S la cual permite obtener otros hidrogramas unitarios con duraciones diferentes. El caudal se expresa mediante la ecuación \[ Q = A * X * Y * Z \].

La formula sugerida en la hoja de cálculo para calcular T_r por Ven Te Chow es \[Tr_chow = 0.00505 \left(\frac{L}{\sqrt{S}}\right)^{0.64}\] conforme al instructivo de CONAGUA.

Después de realizar las operaciones, la fórmula de Chow arroja los siguientes caudales.

Tabla 4.6: Caudales (m³/s) calculados por Chow

Periodo_Retorno	Q_chow
2 años	5.4734
5 años	6.7639
10 años	7.7827
20 años	8.8331
25 años	9.1774
50 años	10.2867
100 años	11.5079
200 años	12.7599
500 años	14.4570
1000 años	15.7696
2000 años	17.1043
5000 años	18.8995
10000 años	20.2787

Se presentan los caudales de las 3 metodologías para poder compararlos y tomar la decisión de que caudal será el recomendado para diseñar las obras de control.

Tabla 4.7: Comparación de caudales (m³/s) por 3 metodologías

	Periodo_Retorno	Q_hut	Q_racional	Q_chow
5	2 años	4.5667	6.5784	5.4734
10	5 años	5.4001	7.3387	6.7639
1	10 años	6.0429	7.9139	7.7827
6	20 años	6.6946	8.4890	8.8331
9	25 años	6.9060	8.6742	9.1774
11	50 años	7.5675	9.2494	10.2867
2	100 años	8.2352	9.8245	11.5079
7	200 años	8.9084	10.3997	12.7599
12	500 años	9.8055	11.1600	14.4570
3	1000 años	10.4889	11.7351	15.7696
8	2000 años	11.1759	12.3103	17.1043
13	5000 años	12.0889	13.0706	18.8995
4	10000 años	12.7828	13.6458	20.2787

La metodología sugerida a usar es la de racional, debido que es la que más se asemeja a las características de la cuenca.

4.2 HIDROGRAMA

Se presenta el hidrograma para el Perído de Retorno de diseño, 10 años. El hidrograma se elaboró siguiendo la metodología racional.

Referencias

Chow, Ven Te, David R. Maidment, and Larry W. Mays. 1994. Hidrología Aplicada. 1st ed. Santafé de Bogotá, Colombia: McGraw-Hill Interamericana, S.A.

———. 2019. Manual de Agua Potable, Alcantarillado y Saneamiento. Drenaje Pluvial Urbano. México, D.F.: Secretaría de Medio Ambiente y Recursos Naturales. https://www.conagua.gob.mx.